Une analyse géométrique du Système Diamond

Géométrie du Système Diamond

(Cliquer sur les graphiques pour agrandir) English

Introduction

Cet article est une réflexion sur le "Système Diamond".

Grâce à sa simplicité, et en dépit de ses imperfections, ce système est très utilisé. Malgré tous mes efforts, je n'ai pas trouvé trace de ses origines, de ses concepteurs, ni de justification de la méthode. J'ai fouillé le Web, interrogé des Grands Joueurs comme Raymond Ceulemans et Francis Connesson, un post sur AzBilliards.com a suscité de l'intérêt mais n'a pas apporté les retours attendus.

Je vais tenter dans cet article d'expliquer d'où peut provenir l'idée de la formule arithmétique et comment le codage des bandes a pu être imaginé.

On s'adresse à des lecteurs familiers du système qui se sont un jour demandé d'où provient la formule magique. On ne le rappelle pas. On n'envisage ni de pointer ses imperfections ni d'indiquer des aménagements. On essaie seulement d'en trouver une justification géométrique, qui découle, selon moi, du principe des "Deux bandes Avant" sur lequel on va revenir en détail.

Préliminaires

Les explications sont basées sur des propriétés géométriques dans un contexte qui n'est pas celui du jeu.

Dans le modèle mathématique les billes sont des points, sans diamètre. Le principe "Réflexion = Incidence" est appliqué en prenant en compte l'effet selon la règle : "un procédé d'effet = une mouche d'écart en largeur", "un procédé d'effet = deux mouches d'écart en longueur". On suppose, ce qui n'est pas réaliste, que l'effet mis au départ est conservé constant dans toute l'intégralité du parcours. On suppose que le contact des billes avec les bandes ne provoque pas de cerclage, ne communique aucun effet.

    Avertissement : Bien entendu, la réalité du jeu est différente et le modèle n'en est qu'une approximation. On va malgré tout, s'efforcer d'en déduire une explication pour la formule et pour le codage du Système Diamond. On va, en particulier, voir pourquoi les repères sur la bande de départ vont de 5 en 5 alors que ceux de la bande de visée vont de 10 en 10.

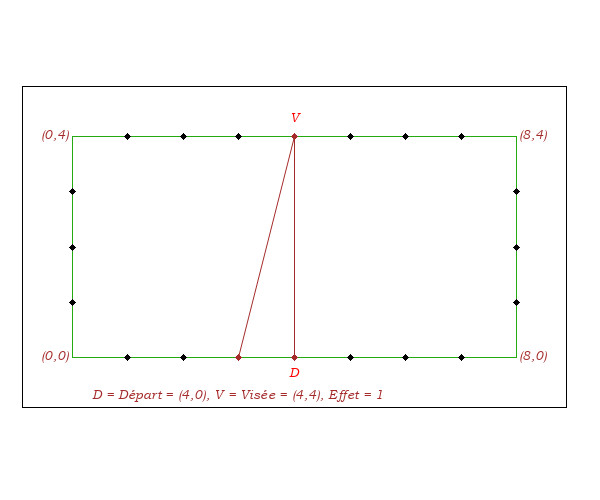
Dans toute la suite, les points (géométriques) des schémas et des exemples sont repérés par les coordonnées dans le système cartésien dont les axes sont la grande bande du bas (les x) et la petite bande de gauche (les y):

L'origine (0,0) est placé au coin en bas à gauche de la table. Les coordonnées du coin en haut à gauche sont (0,4), celles du coin en bas à droite (8,0) et celles du dernier coin (8,4).

L'effet est pris en compte selon :


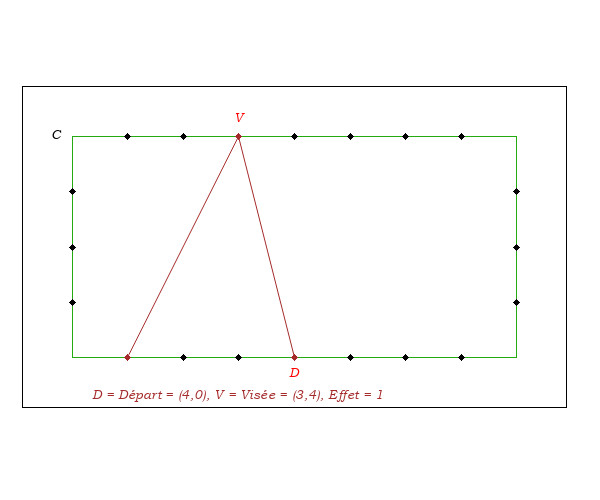
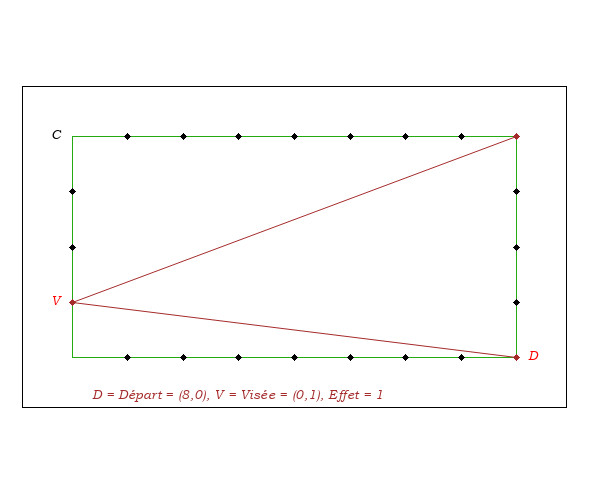
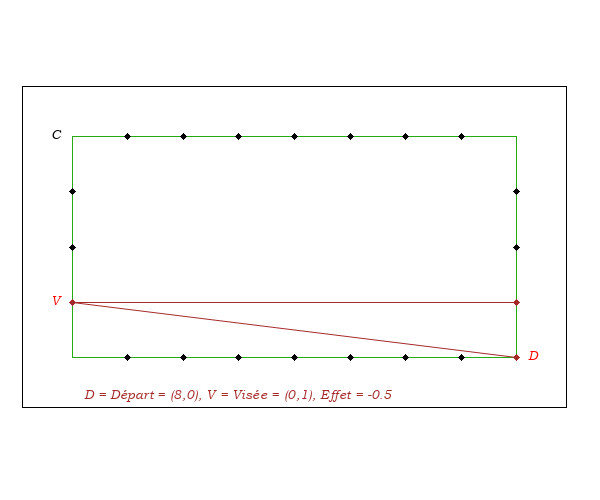
I- Deux Bandes Avant

La recette du "Deux Bandes Avant" est la suivante :

En jouant sans effet, si on touche à une distance "d" du coin, on arrive sur la troisième bande à une distance "2d" du point départ.

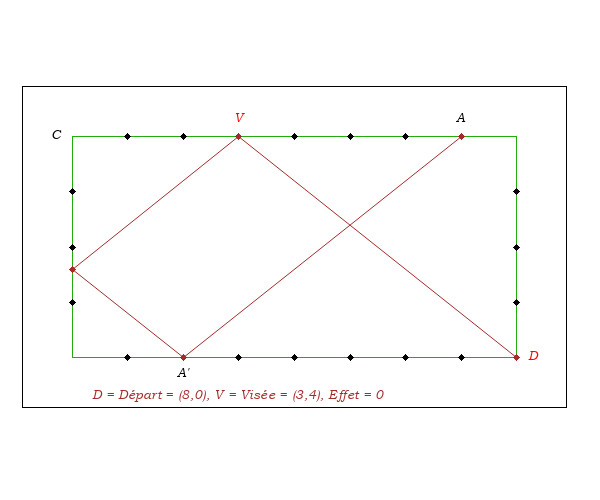
Nous allons justifier la recette quand l'attaque fait un angle de 45 degrés par rapport aux bandes et quand le point de départ et la visée sont sur deux bandes parallèles. Et voir que, en dehors de ces deux cas, elle est inexacte.

    Considérons sur la figure ci-contre les triangles

    VCV', VCR

    Ils sont égaux et rectangles en C. Tous les angles verts sont égaux à cause du principe "Réflexion = Incidence". Les droites DV et RA sont parallèles. La distance DA est égale à la distance V'R. Il en résulte que

    La distance DA est double de la distance CR
    		   

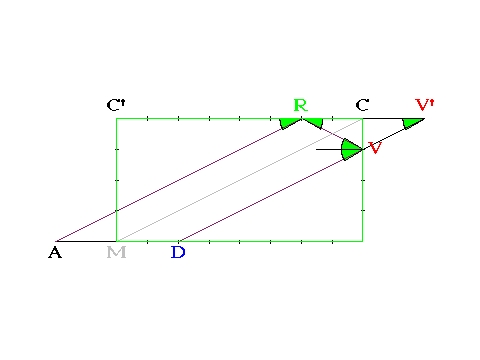
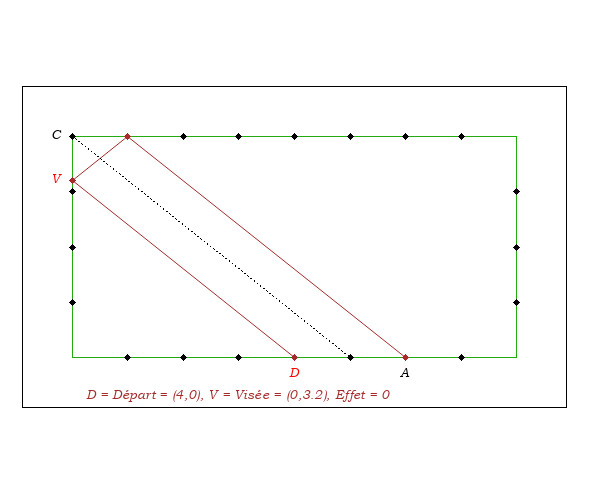
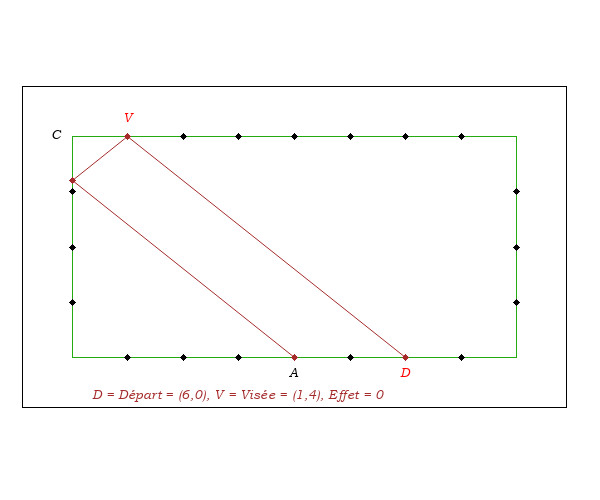
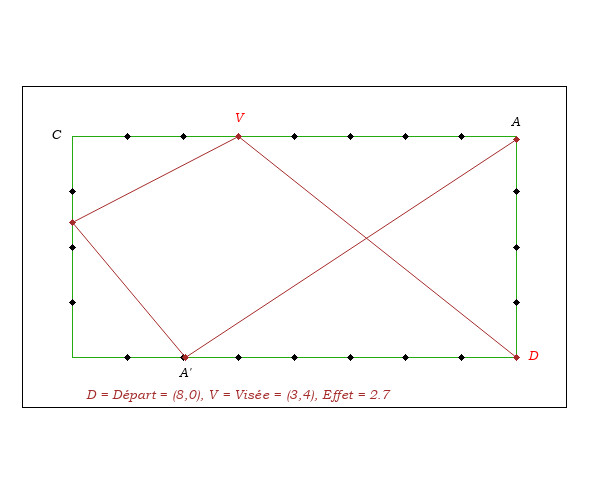
  1. On remarque que pour pouvoir affirmer que DA est double de la distance CR, il convient que DA et CR soient parallèles.
  2. On remarque aussi que DA n'est le double de CV que si le triangle VCR est triangle isocèle, c'est-à-dire que si la direction DV fait un angle de 45 degrés par rapport aux bandes.
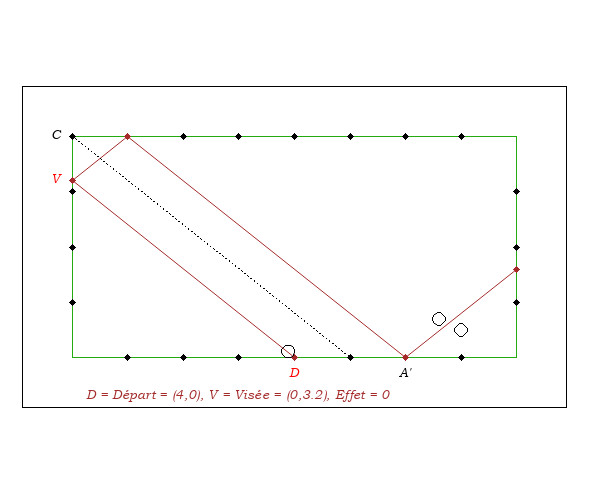
  3. Sur la figure ci-dessus, en imaginant que le point de départ est en A, l'arrivée en D, A et D étant sur deux bandes parallèles, la distance DA étant de 4 mouches, on vise en R à 2 mouches de C.
  4. Sur la figure ci-dessus, en imaginant que le point de départ soit en D, l'arrivée en A, à 4 mouches de D, Il ne faut pas viser sur la petite bande à 2 mouches du coin car la visée et le point de départ ne sont pas sur deux bandes parallèles et parce que DV n'est pas à 45 degrés.
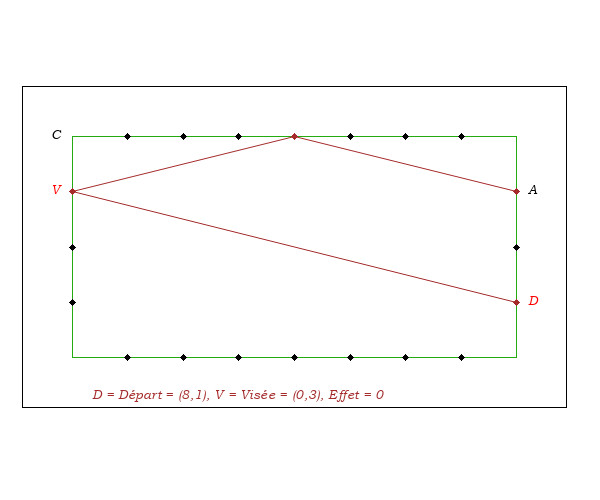
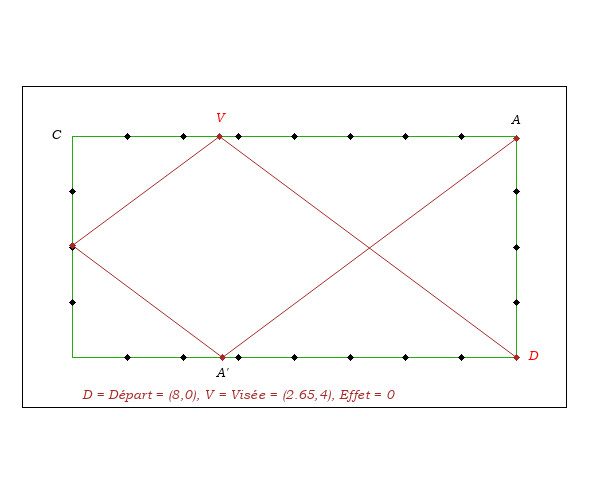
  5. Pour déterminer la visée (du coup sans effet), on remarque que la médiane MC du triangle DCA est parallèle aux droites DV et AR. En conditions de jeu, cette propriété permet de déterminer la visée V, car il est assez facile de visualiser la médiane MC et sa parallèle DV.

Illustration
Exemple 1- Départ grande bande en D = (3,0), on souhaite arriver grande bande à deux mouches de D en A = (5,0). La recette indique que l'on doit viser petite bande à une mouche du coin en V = (0,3). La trajectoire DV est à 45 degrés. On constate que le résultat est correct.
Exemple 2- Départ grande bande en D = (4,0), on souhaite arriver grande bande en A = (6,0) à deux mouches de D. Si on utilise mal la recette et que l'on vise petite bande à une mouche du coin en V = (0,3), la trajectoire DV n'étant pas à 45 degrés, les segments DA et CV n'étant pas parallèles, le résultat n'est pas bon.
Exemple 3- On reprend l'exemple 2-. On vise petite bande en V = (0,3) et on ajoute de l'effet. Le résultat est bon.

Exemple 4- On reprend l'exemple 2- en jouant sans effet. En utilisant la méthode de la médiane on visualise V = (0,3.2). Le résultat est bon.

Exemple 5- Départ grande bande en D = (6,0), on souhaite arriver à deux mouches en A = (4,0). On peut utiliser la recette car VC et DA sont parallèles. On vise grande bande du haut à une mouche en V = (1,4). Le résultat est bon.
Exemple 6- Départ petite bande en D = (8,1), on souhaite arriver petite bande à deux mouches de D en A = (8,3). En utilisant la recette on vise petite bande à une mouche du coin, en V = (0,3). VC et DA sont parallèles. Le résultat est bon.

II- Trois Bandes Avant

Exemple 7- Supposons que l'on veuille jouer en 3 bandes avant sans effet le point du schéma ci-contre. Le départ est en D = (6,0). Au jugé, on voit qu'on pourrait arriver sur la 3ème bande à deux mouches du point de départ en A' = (4,0). Avec la recette "Deux bandes avant", D et V étant sur des bandes parallèles, on vise exactement à une mouche du coin grande bande, en V = (1,4). Le résultat est bon.
Exemple 8- Supposons que l'on veuille jouer en 3 bandes avant sans effet le point ci-contre. Le départ est en D = (4,0). Au jugé, on voit qu'on pourrait arriver sur la 3ème bande à deux mouches en avant du point de départ en A' = (6,0). Avec la recette "Deux bandes avant", en s'aidant de la direction de la "médiane", on vise petite bande, en V = (0,3.2). On arrive en A' = (6,0) comme souhaité.

III- Système Diamond

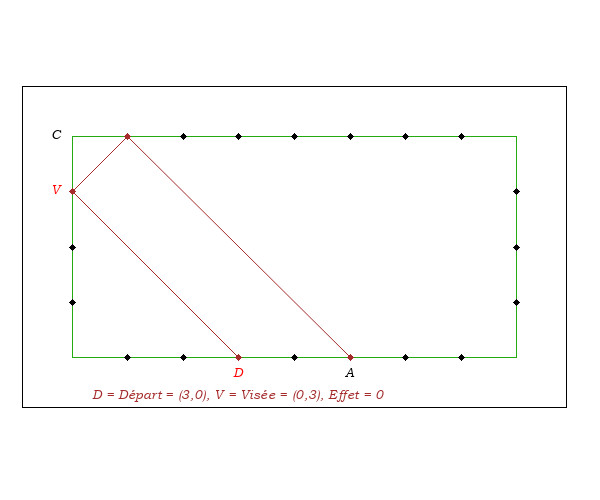
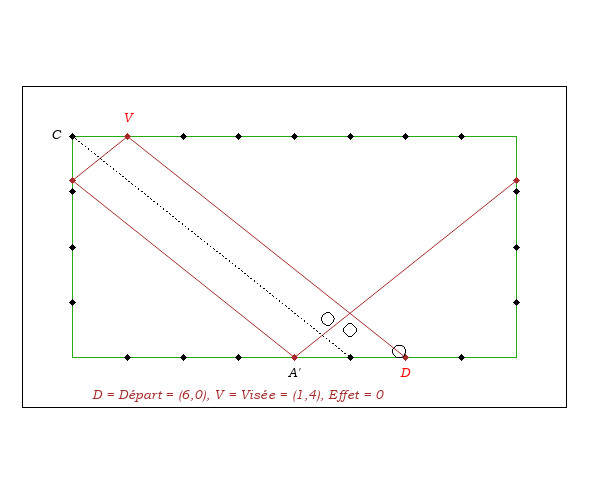
On suppose que le "Système Diamond" est familier au lecteur. (Eventuellement voir les annexes). On envisage de comprendre son codage et sa formule de calcul.

Exemple 9- Considérons un départ au coin en bas à droite en D = (8,0) = Diamond 50, une visée grande bande du haut en V = (3,4) = Diamond 30. Jouons sans effet.

On touche la grande bande du bas (3ème bande) en A' = (2,0) = Diamond 20, à 6 mouches du départ, conformément à la recette "Deux bandes avant", D et V étant sur des bandes parallèles.

On constate que le manque d'effet nous fait arriver sur la 4ème bande en A = (7,4) = Diamond 10.



Inversement, toujours départ au coin, en supposant que notre objectif soit d'arriver 3ème bande en A' = (2,0), compte tenu de la recette "Deux bandes avant", la visée est choisie en V = (3,0).

On remarque la relation distance(C,V) = 3= distance(D,A')/2.

Avec comme unité "1 mouche = 5" sur la bande de départ et "1 mouche = 10" sur la bande de visée, en codant grande bande départ le coin (0,0) par 10, et bande de visée le coin (0,4) par 0, la formule ci-dessus s'écrit

V(30) = D(50) - A'(20).

et le codage

Départ101520253035404550
Visée01020304050xxxxxx

C'est le codage Diamond pour Départ et Visée. Avec ce codage, A', étant l'arrivée sur la 3ème bande, la visée est donnée par

V = D - A'

Nous avons une formule, un codage pour le départ et un codage pour la visée. Nous avons fait un pas vers le système Diamond. Mais nous n'avons encore rien sur l'essentiel, à savoir l'arrivée sur le 4ème bande.

Un premier système qui ne marche pas

On joue sans effet.

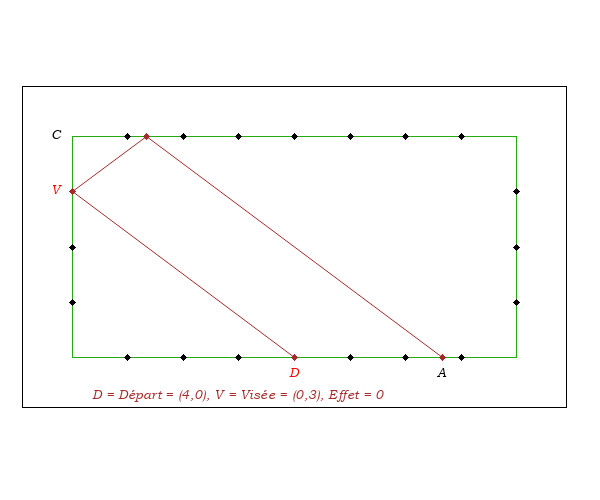
On a vu, exemple 9-, que départ en D = Diamond 50, visée en V = Diamond 30, donne une arrivée 4ème bande en A = (7,0) et non au coin (8,4).

Pour arriver en A = (8,4), on constate qu'il faut allonger en visant V = (2.65,4) = Diamond 26.5. L'arrivée 3ème bande est alors en A' = (2.70,0) = Diamond 23.50.

On pourrait décider de coder ce coin A par 23.5. De ce fait la formule V = D - A donnerait la visée correcte et le résultat souhaité pour le départ D = (8,0) = Diamond 50.

Malheureusement, l'utilisation de la formule et de ce codage, convenable pour le départ précédent D = 50, ne convient plus pour un départ en D = (7,0) = Diamond 45, ni pour D = (6,0) = Diamond 40, ni pour D = (5,0) = Diamond 35 .... L'arrivée 4ème bande s'écarte de plus en plus du coin. L'arrivée A' 3ème bande ne varie pas, mais les lignes d'arrivée A'A tournent sensiblement.

Jouons plein effet

Exemple 10- Départ D = (8,0) = Diamond 50, visée en V = (3,4) = Diamond 30, effet = 2.7

On arrive sur la 3ème bande en A' un peu à droite de (2,0) = Diamond 20. L'effet produit son œuvre. On arrive sur la 4ème bande en A = (8,4) = Diamond 20.

On code le coin A = (8,4) = Diamond 20 par 20. La formule V = D - A donne la visée correcte.

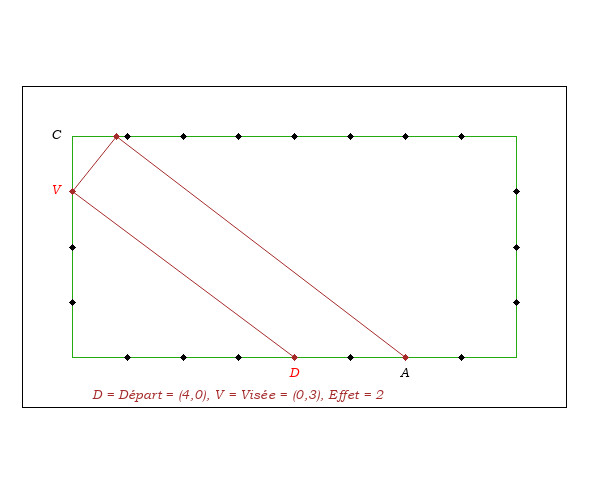
On constate deux choses

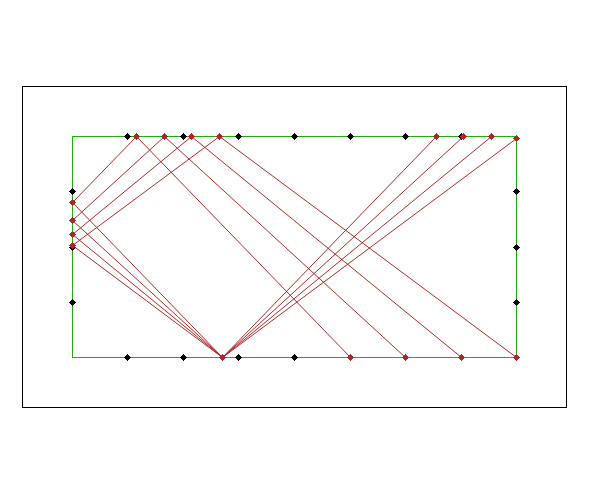
  1. en faisant varier le point de départ, en visant selon V = D - A(20), les lignes d'arrivée A'A sont très stables. Et il en est de même pour les arrivées autres que A = Diamond 20.
  2. l'effet ne fait pas beaucoup varier l'arrivée 3ème bande A' car il y a compensation entre l'allongement sur la bande de visée et le raccoucisement qui en découle sur la 2ème bande.

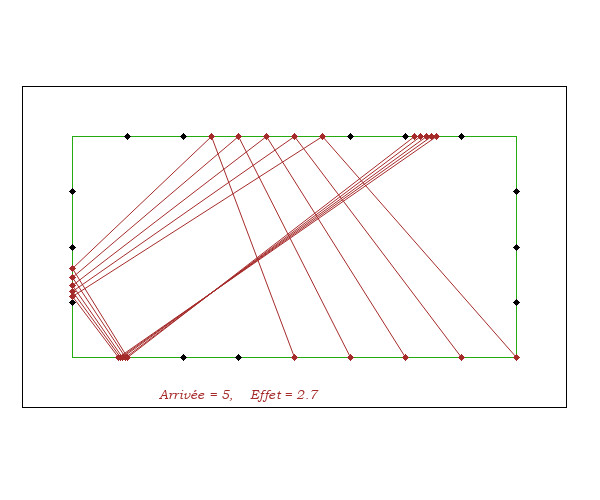
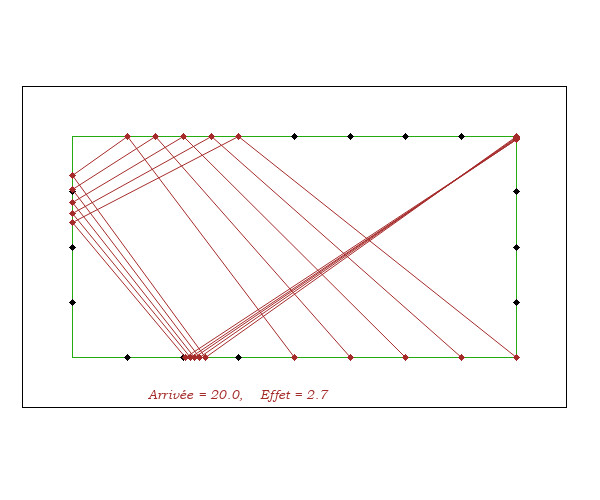
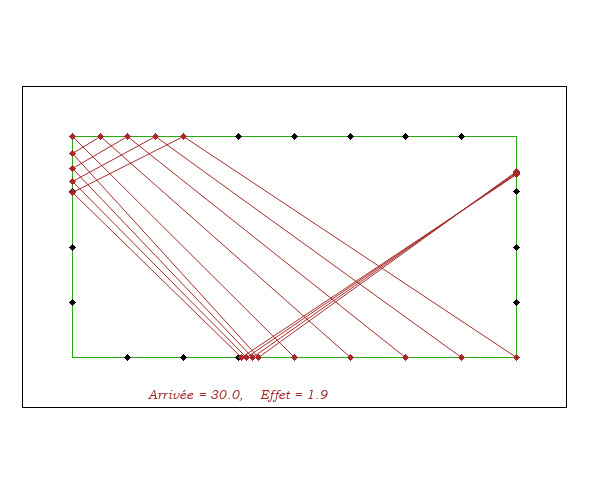
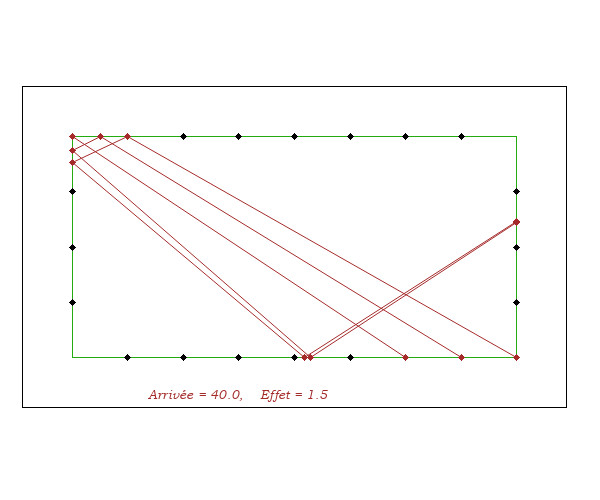
Cela permet de coder l'arrivée 4ème bande A avec le (ou en fonction du) code de celui de l'arrivée A' 3ème bande.

C'est le "Système Diamond" !!!

Conclusion

Nous avons mis en évidence des faits majeurs qui expliquent le système :

  1. Grâce au codage indiqué ci-dessus, le départ D, la visée V, l'arrivée A' sur la 3ème bande sont liés par une formule simple V = D - A' (démontrée dans le cas du sans effet).
  2. Les lignes d'arrivées A'A sont stables avec du plein effet.
  3. De ce fait, on peut définir le code de A en fonction du code de l'arrivée A' sur la 3ème bande et utiliser la formule V = D - A.


Annexes
  1. Croquis des repères et des lignes d'arrivées
  2. Explications détaillées du Système (Billard Club Sottevillais)

Remerciements à Diane.A et à Marie.B pour leur contribution.