3-Cushion Bank Shot, Diamond System
| (Click on the graphics to enlarge) |
 French French
|
Introduction
This article is a geometric analysis of the "Diamond System".
Thanks to its simplicity, and despite its imperfections, this system is widely used. Despite efforts, I could not find any trace of its origins, its creators, or justification for the method. I have searched the Internet, questioned top players like Raymond Ceulemans and Francis Connesson, a post on AzBilliards.com rolled up interest but did not provide the expected feedback.
In this article, I will try to explain from where the principle of the arithmetic formula is coming and how the rails codes may have been conceived.
This is targetting readers familiar with the system who have once day wondered from where the magic formula was coming. We will not recall it, nor will we point out its imperfections nor suggest adjustments. We will merely attempt to find a geometric justification for it, which, according to me, derives from the principle of "2-Cushion Bank Shot", which we will now examine in detail.
Preliminaries
The explanations are based on geometric properties in a different context from the game itself.
In the mathematical model, the balls are points, with no diameter. The principle "Reflection = Incidence" is applied, taking into account the side spin according to the rule: "one tip of spin = one diamond of deviation in width", "one tip of spin = two diamonds of deviation in length". We assume, which is unrealistic, that the spin applied at the shot remains constant throughout the entire trajectory. We also assume that contact with the rails does not cause any hooping, and does not communicate any additional spin.
|
Warning : Of course, the reality of the game is different and the model is only an approximation of it. Nevertheless we will try to get geometric explanations for the formula and for the codes of the Diamond System. In particular, we will explain why the markers on the starting cushion go from 5 to 5 while that of the aiming cushion go from 10 to 10. |
In the following, the (geometric) points of diagrams and examples are identified by their coordinates in the Cartesian system whose axes are the bottom long rail (x's) and the short left rail (y's):
The origin (0,0) is at the bottom left corner of the table. The
coordinates of the top left corner are (0,4), those of the bottom right corner
(8,0) and those of the last corner (8,4).
The spin is taken into account according to:
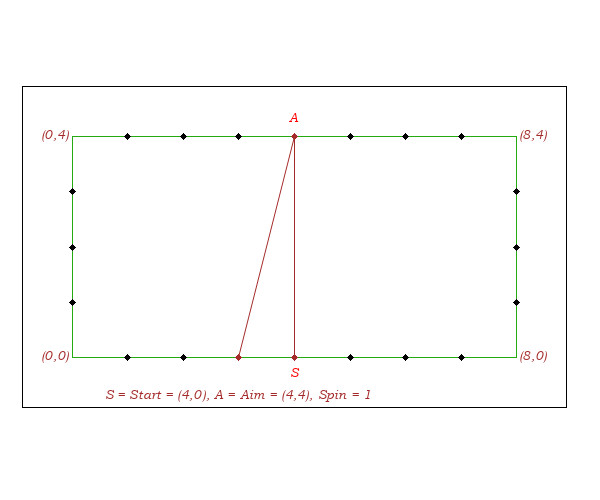
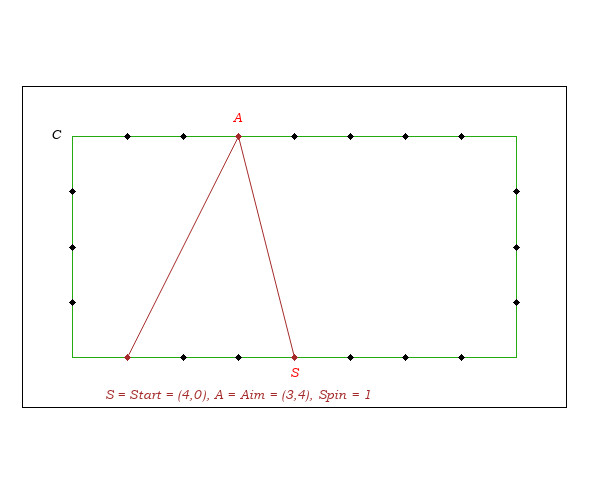
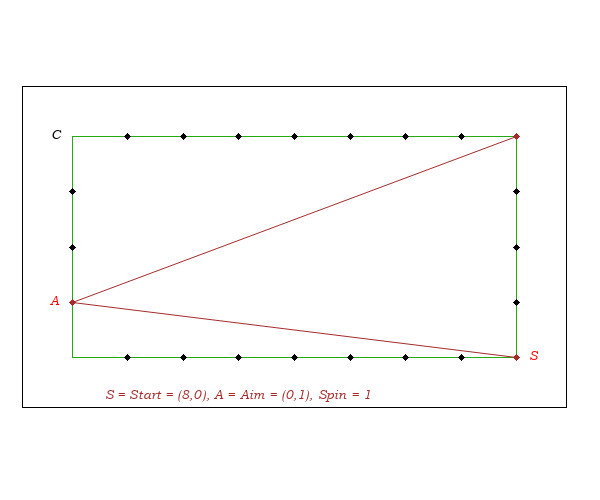

I- 2-Cushion Bank Shot
The "2-Cushion Bank Shot" recipe is as follows:
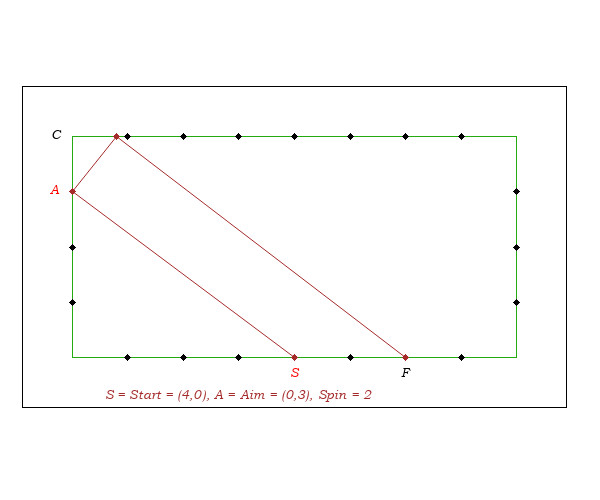
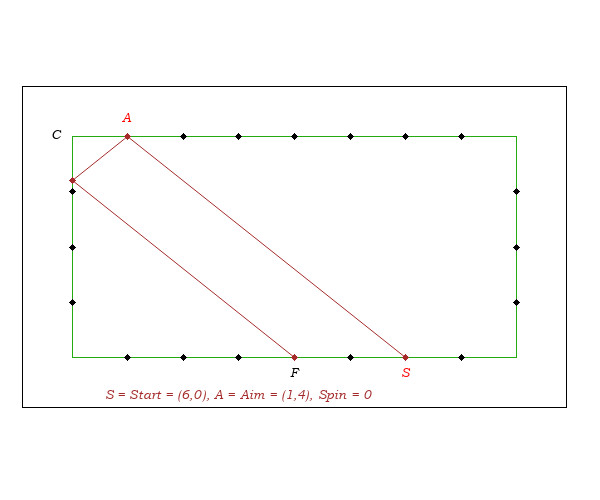
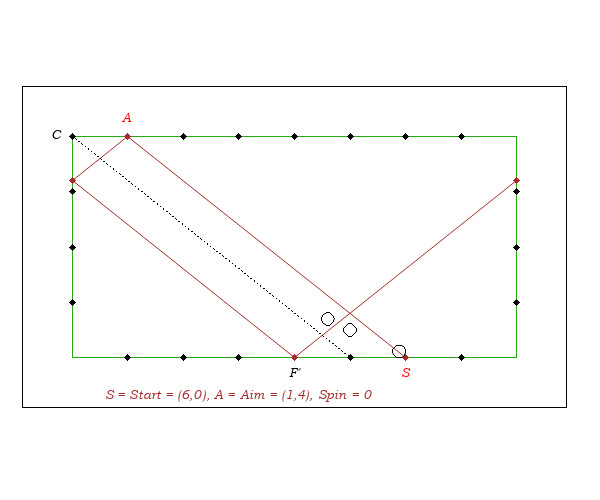
Playing with no side spin, if we hit at a distance "d" from the corner, we end on the third rail at a distance "2d" from the starting point.
We will justify this rule when the shot makes a 45-degrees angle with the rails and when the starting point and the aim are on two parallel rails. We will also see that outside these two cases, the rule is inaccurate.
- Note that to be able to state that SF is twice CR, it is necessary that SF and CR are parallel.
- Note as well that SF is twice CA only in case the triangle ACR is isosceles, that is, if the direction SA is 45-degrees with respect to the cushions.
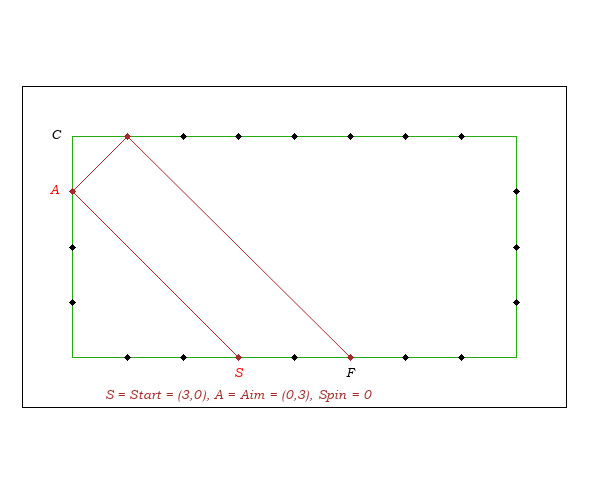
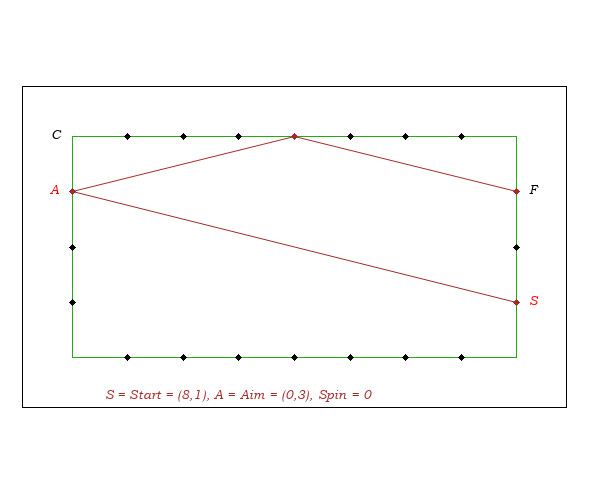
- In the figure above, imagining the starting point is F and end is S. R and S being on two parallel cushions, the distance SF being 4 diamonds, we aim R, 2 diamonds from C.
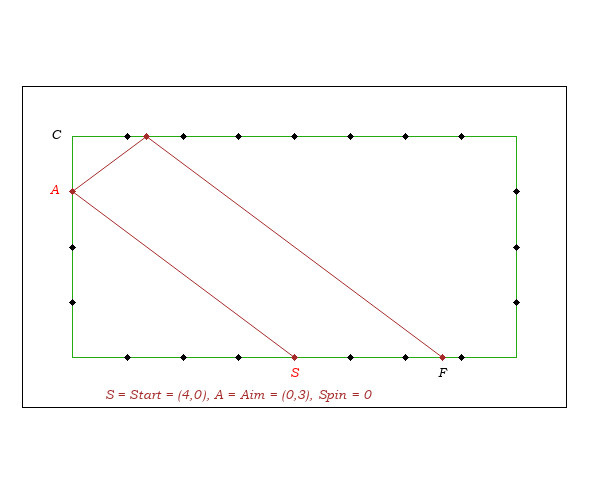
- In the figure above, imagining the starting point is S and end is F, 4 diamonds from S. We must not aim the short cushion 2 diamonds from the corner because the aim and the starting point are not on two parallel cushions and because SA is not 45-degrees.
- To determine the aim (no spin), we note that the median MC of the triangle SCF is parallel to the lines SA and FR. In game conditions, this property gives a way to determine the aim A, because it is quite easy to visualize the median MC and its parallel SA.
Illustration
II- 3-Cushion Bank Shot
III- Diamond System
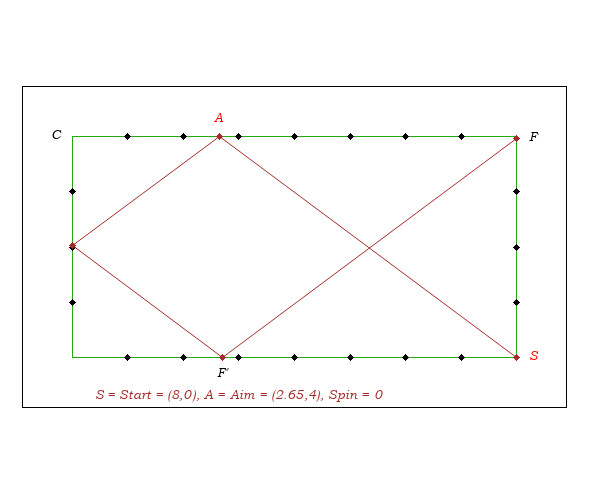
We assume that the reader is familiar with the (corner 50) "Diamond System". (Possibly look at the annexes). We expect to understand its codes and its calculation formula.Conversely, starting S = (8,0) = Diamond 50, let's assume that our objective is finish 3rd rail F' = (2,0). We see that for that, according the "2-Cushion Bank Shot" recipe, we have to aim A = (3,0).
We note the relation distance(C,A) = distance(S,F')/2.
With unit "1 diamond = 5" on the starting rail and "1 diamond = 10" on the aiming rail, with code 10 for the corner (0,0) on the start rail, and code 0 for the corner (0,4) on the aiming rail, the formula becomes
and the codes
| Start | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| Aim | 0 | 10 | 20 | 30 | 40 | 50 | xx | xx | xx |
That is the Diamond codes for Start and Aim. With these, F', being the arrival on the 3rd rail, the aim is given by
We got a formula, codes for the start rail and codes for the aim rail.
We got a step towards the Diamond system. But we have not yet achieved anything on the essential, namely the end on 4th rail.
A first system that does not work
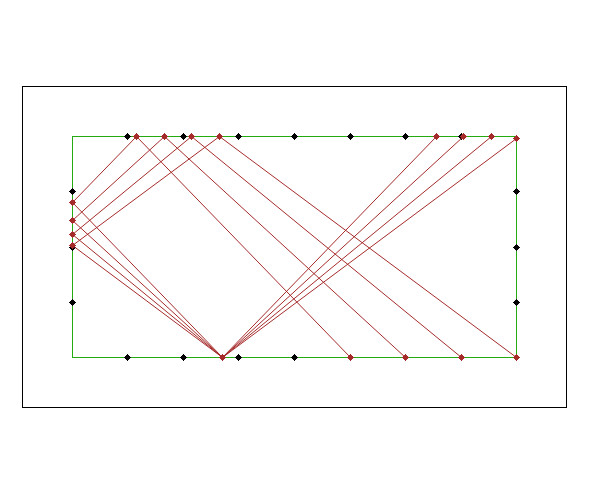
Let's play no spin.
Now let's play full side spin.
We can highlight two points
- By varying starting points, aiming according to A = S - F(20), the finish lines F'F are very stable. And that it is the same for arrivals other than F = Diamond 20.
- The spin does not affect much the arrival F' on the 3rd cushion because there is compensation between elongation on the aim rail and shortening on the 2nd rail.
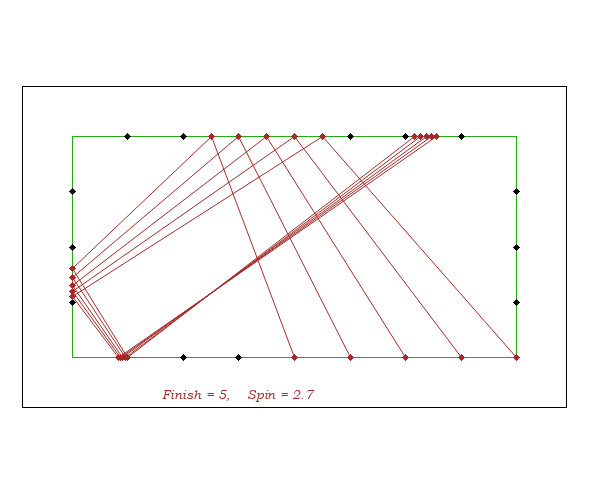
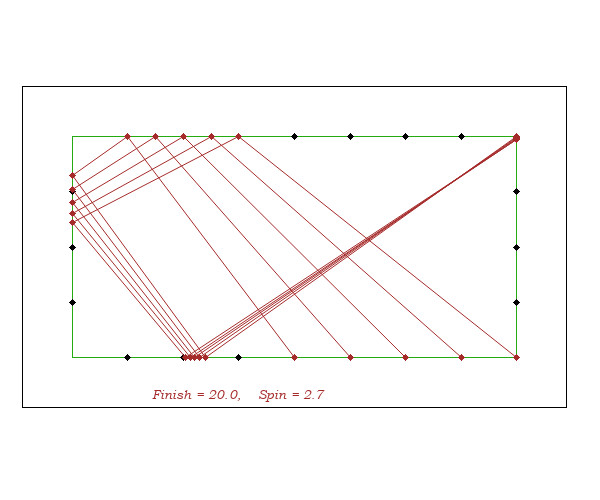
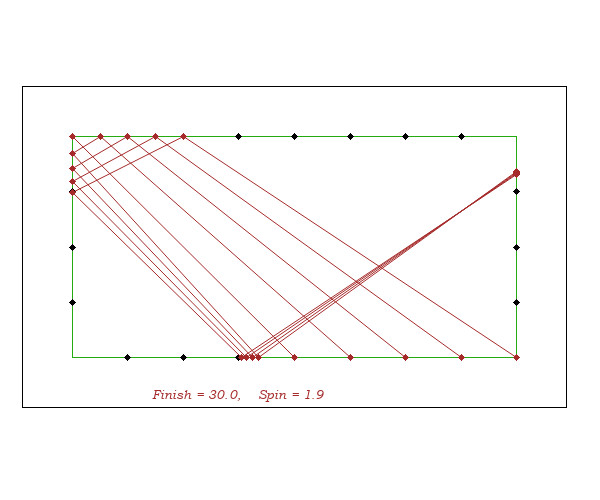
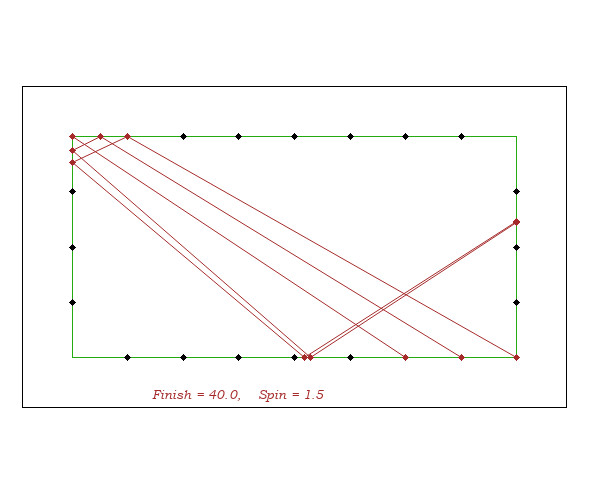
This allows to define the 4th cushion end F marker by the (or depending on the) code of that of 3rd rail end F'.
That is the "Diamond System" !!!
Conclusion
We have highlighted major facts explaining the system:
- Thanks to the above codes, the start S, aim A, and arrival F' on the third rail are linked by a simple formula A = S - F' (proved in case no spin).
- The finish lines F'F remain stable with full spin.
- Therefore we can define the code of finish F based on the code of the third rail arrival F' and use the formula A = S - F.
Annexes
- Markers and Finish lines diagram
- Detailed explanations of the System (Sotteville Billard Club)
Many thanks to Diane.A and Marie.B for contribution.